Dot product and cross product are two mathematical operations that are frequently used in linear algebra and vector calculus. So, what is the difference between dot product and cross product?
The resultant of dot product is a scalar quantity. And, the resultant of cross product is a vector quantity. Not to mention, one of the most significant similarities between them is that they both follow the scalar multiplication law.
Dot Product vs Cross Product
| Dot Product | Cross Product | |
| 1. | The resultant of dot product is a scalar quantity. | The resultant of cross product is a vector quantity. |
| 2. | Dot product is product of magnitude of vectors & cosine of angle between them. | Cross product is product of magnitude of vectors & sine of angle between them. |
| 3. | The dot product of vectors does not have any direction because it’s a scalar. | The direction of the cross product of vectors is given by the right-hand rule. |
| 4. | Mathematically, the dot product is represented by A . B = A B Cos θ | Mathematically, the cross product is represented by A × B = A B Sin θ |
| 5. | If the vectors are perpendicular to each other then their dot product is zero i.e A . B = 0 | If the vectors are parallel to each other then their cross product is zero i.e A × B = 0 |
| 6. | The dot product strictly follows commutative law. | The cross-product does not follow commutative law. |
| 7. | The dot products are distributive over addition. | The cross products are also distributive over addition. |
| 8. | They follow the scalar multiplication law. | They too follow the scalar multiplication law. |
| 9. | They are Symmetric. | They are anti-symmetric. |
| 10. | Applications of dot products are in finding projections, work done by a force, etc. | Applications of cross-product are in computing torque, finding the moment of inertia, etc. |
What is Dot Product?
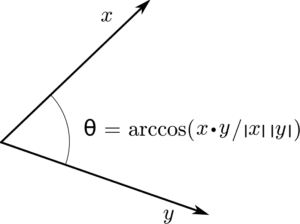
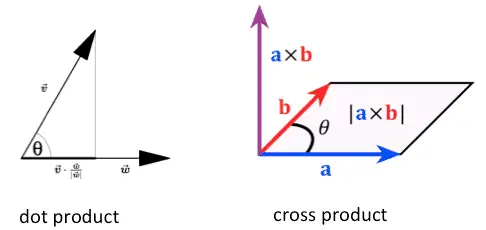
The dot product is nothing but a product of the magnitude of the vectors and the cosine of the angle between them. The resultant of the dot product of vectors is always a scalar quantity. Hence, the resultant has only magnitude.
In order to align the vectors in the same direction, we take the cosine of the angle between vectors. As a result, the resultant of the dot product of vectors does not have any direction, hence, also known as the scalar product.
Apart from being known as a scalar product, the dot product also goes by the name of the inner product or simply the projection product.
Dot Product Formula
According to the dot product definition, there are two ways to write the dot product formula. Let us get to know them one by one in detail.
Algebraic Definition
Suppose there are two vectors;
where,
a = [a1, a2, a3, ….., an]
b = [b1, b2, b3, ……, bn]
According to the algebraic definition, the vector dot product formula is
A . B = ∑ ai . bi = a1b1 + a2b2 + a3b3 + …… + anbn
where,
∑ = summation
n = dimension of the vector space.
Geometric Definition
According to the geometric definition, the vector inner product or scalar product formula is:
A · Β = |A| |B| cos θ
where,
A and B are Euclidean vectors
θ is the angle between vectors.
Special Mention
While calculating the vector dot product, the following set of rules should be kept in mind.
- i . i = 1, i . j = 0, i . k = 0
- j . i = 0, j . j = 1, j . k = 0
- k . i = 0, k . j = 0, k . k = 1
where,
i, j, and k are the unit vectors in x, y,and z directions.
Properties of Dot Product
Apart from being scalar in nature, a dot product has the following properties:
Commutative
Dot products or vector inner products are commutative in nature.
A · Β = |A| |B| cos θ = |B| |A| cos θ = A . B Or, simply A .B = B . A
Distributive
Dot products are distributive in nature.
Α · (B+C) = A · B + A · C
Scalar Multiplication Law
Dot products strictly follow the scalar multiplication law.
(μA) . (νB) = μν (A . B)
Orthogonal
The dot product of two vectors is orthogonal, only and only if, their product is zero.
θ = 90°. A . B = 0
Applications of Dot Product
Applications of dot product include:
- Finding the Angle Between Two Vectors
- Finding Projections
- Work Done by a Force
- Testing for Orthogonality
- Finding the Magnitude of a Vector
- Determining the Direction of a Force, etc.
What is Cross Product?
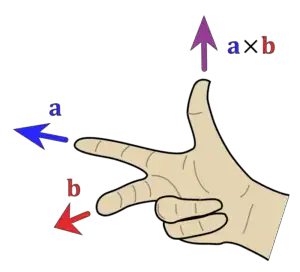
A vector cross product is nothing but a product of the magnitude of the vectors and the sine of the angle between them. The resultant of the cross product of vectors is always a vector quantity, that’s why also known as the vector product.
Hence, the resultant has magnitude as well as direction. The resultant vector of the cross product of two vectors is always perpendicular. Therefore, the direction of the cross-product of vectors can be determined by the right-hand rule.
Apart from being known as a vector product, the vector cross product also goes by the name of the directed area product.
Cross Product Formula
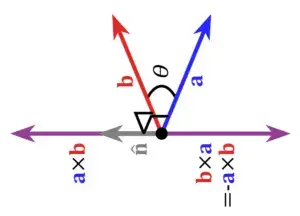
The vector cross-product formula is defined as:
A × Β = |A| |B| sin θ n
where,
A and B are two vectors
θ is the angle between A and B
|A| and |B| are the magnitudes of the two vectors
n is the unit vector perpendicular to the plane containing A and B.
Special Mention
While calculating the vector or cross product, the following set of rules should be kept in mind.
- i × j = k
- j × k = i
- k × i = j
where
i, j, k are the unit vectors in x, y, and z-direction.
Properties of Cross Product
Apart from being vector in nature, a cross-product has the following properties:
Non-Commutative
Cross-products are non-commutative in nature.
A × B ≠ B × A
Distributive
Just like dot products, cross products are also distributive in nature.
A × (B + C) = (A × B) + (A × C)
Scalar Multiplication Law
Cross products are also compatible with scalar multiplication law.
(μA) × (B) = μ (A × B)
Orthogonal
The cross product of two vectors is orthogonal, only and only if, their product is maximum.
θ = 90°
Applications of Cross Product
Applications of Cross Product include:
- Determining the Area of a Parallelogram
- Computing Torque
- Finding the Moment of Inertia
- Magnetic Field
- Calculating the Normal Vector
- Computing Angular Momentum, etc.
That’s it for this post. If you like this article, share it if you like, like it if you share it. You can also find us on Mix, Twitter, Pinterest, and Facebook. Hey man, If you have come this far, do give us feedback in the comment section. It would make my day. You can also make a donation. Your donations will help us to run our website and serve you BETTER. Cheers!!!
You might also like:
- Scalar Quantity Definition in Physics, its Types, Properties, Solved Examples
- Vector Quantity – Definition, Types, Properties, Solved Examples
- Dot Product – Definition, Types, Properties, and Solved Examples
- Cross Product – Definition, Right-Hand Rule, Properties, and solved examples
- Difference Between Scalar and Vector Quantity
Simply great
its simply great!!!
Nice
Understood dot product and cross product. Thank you
welcome, keep visiting us…!!!