Dot Product – Definition, Types, Properties, and Solved Examples

Finding solutions to certain problems is not always with a simple multiplication of two or more terms. The difference arises when a term represents more than just a number.

Vectors are such terms that represent two factors, and not just one numerical. They are magnitude and direction.

So, to multiple vectors, there are broadly two methods to go about. The first is the Dot Product that we will discuss below, and the second is the Cross Product.

What is a Dot Product?

The name Dot Product is because of the ‘.’ present between two terms instead of the usual ‘x’ sign. They often represent the vector lengths as their magnitudes and the angles between those magnitudes.

Definition

It can be defined under two separate headings, applicable in 2 different ways: Algebraic and Geometric. The method that follows is significantly different

Algebraic Dot Product

It is the simpler one of the two. An Algebraic dot product can be defined as the addition of the two terms. Each term can itself be a solution to an algebraic operation.

Geometric Dot Product

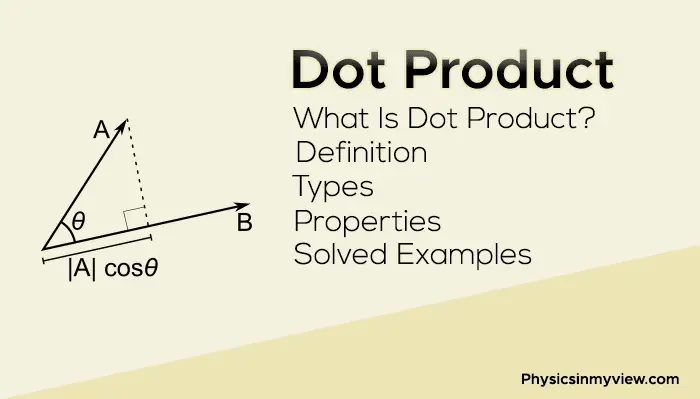
A Geometric Dot Product is the product of two vector magnitudes and the angle between them, cosine.

Properties

Property 1: Algebraic Dot Product = Geometric Dot Product in the final answer you get.

Property 2: If the angle between the two terms is 0°, then the cosine value is 1. This implies that the terms are parallel to each other.

On the other hand, if the angle between the two terms is 90°, the cosine value is 1/2. This implies that the terms are perpendicular to each other.

Property 3: Since dot product is a scalar product, therefore, (pa).(qb)=(pb).(qa)=pq a.b. Here p and q represent the length of the two terms a and b from the point of origin.

Property 4: If the dot product between one vector and with itself, for example, a with a or b with b is calculated, then a.a = a.a cos 0 = a2 or b.b = b.b cos0

Property 5: Both Algebraic and Geometric abide by the distributive law – a.(b + c) = a.b + a.c

The following two properties are based on coordinates of the x-axis, y-axis, and z-axis, represented as i, j, and k.

Formula

Since they are defined on different principles, their formulae are also different. While one is a summation, the other is a mixed expression that involves incorporating the angle.

Algebraic Dot Product

The Algebraic Dot Product is represented as –

a · b = ax × bx + ay × by

Where a is the first term
b is the second term

Here, ax and ay are the two different values of the same term, but in different dimensions of the x-axis and y-axis, respectively. For bx and by, too, the expressions represent the values in the two different dimensions.

Geometric Dot Product

The Geometric Dot Product is represented as –

a · b = |a| × |b| × cos(θ)

Where a and b are the two terms.
θ is the angle between the two terms.

Unlike the Algebraic Dot Product, the Geometric Dot Product does not have a two-dimensional representation; only one value for one term. However, the addition here is the inclusion of the cosine angle between the two terms.

Solved Examples

Algebraic Dot Product

Example: The coordinates for the x and y for the vectors terms a and b are given as – (-2,6) and (3,12)

Solution: Substituting the given values in the formula of a · b = ax × bx + ay × by

We get –

a . b = (-2 × 3) + (6 × 12)
a . b = (-6) + (72)
a . b = -6 + 96
a . b = 90

So, the dot product of the terms a and b by the Algebraic Dot Product Method is 90.

Geometric Dot Product

Example: The angle is 90°. Along with it, the given a and b values are 19 and 16.

Solution: Substitute the given values in the formula of a . b = |a| x |b| x cos (θ)

We get –

a . b = |19| x |16| x cos (90)
a . b = |19| x |16| x 1/2
a . b = 19 × 16 × 1/2
a . b = 152

So, the dot product of the terms a and b by the Geometric Dot Product Method is 304.

Conclusion

It is essential to understand the difference between what is a dot product, its properties, and its formulae to differentiate it from other product-finding methods. Interchanging of dot and cross products is not possible as they are very different in their characteristics.

That’s it for this post. If you like this article, share it if you like, like it if you share it. You can also find us on Mix, Twitter, Pinterest, and Facebook. Hey man, If you have come this far, do give us feedback in the comment section. It would make my day. You can also make a donation. Your donations will help us to run our website and serve you BETTER. Cheers!!!

You might also like:

• Scalar Quantity – Definition, Types, Properties, Solved Examples
• Vector Quantity – Definition, Types, Properties, Solved Examples
• Cross Product – Definition, Cross Product For Two Vectors, Right-Hand Rule, Properties, and solved examples